Base de connaissances Šikula Robotik

Passage au PID numérique

par Florent, février 2014

Cet article présente l’utilisation d’un PID numérique minimisant les calculs réalisés par un microcontrôleur pour atteindre les mêmes performances qu’un filtre d’asservissement PID classique. Nous verrons, sans les détailler, les principes généraux qui mènent au filtre numérique, dont la formulation est particulièrement adaptée au mode de calcul des processeurs. Nous mettrons ensuite cette formule en pratique avec une classe C++. Le lecteur n’étant pas intéressé par les fondements théoriques pourra sans difficulté utiliser le résultat final.

La transformée en Z pour les systèmes en temps discret

Les systèmes à microprocesseurs ont la particularité de travailler en temps discret, c’est-à-dire qu’ils découpent le temps en intervalles pendant lesquels ils n’ont qu’une seule mesure du système supervisé. Le signal est échantillonné et le comportement entre deux échantillons est inaccessible. Toutefois, si la période est suffisamment faible au regard de la dynamique du signal observé, le comportement hors échantillons peut souvent être négligé.

Pour traduire l’évolution temporelle des systèmes échantillonnés, la transformée en Z est un outil mathématique commode. Elle repose sur une fréquence d’échantillonnage fixe caractérisée par une période T. Mathématiquement F(z), transformée en Z de f, peut être définie à partir de la transformée de Laplace de variable s :

$F(z) = {{\mathcal{L}[f(t)]}_{ s={{ln z}\over{T}}}} = \sum\limits_{k \in \mathbb{Z}} f(kT) z^{-k}$

Transformée en Z de f

La seconde notation sous la forme d’une somme est cependant plus simple à comprendre : le signal est constitué d’un ensemble d’échantillons pris au temps k×T, la variable z servant à indiquer le décalage temporel (retard) dans le signal. Les exemples simples qui suivent permettent de représenter graphiquement le concept.

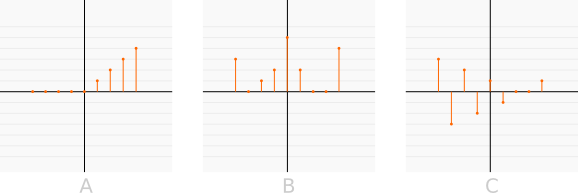
Exemples de signaux.
A(z) = z^-1 + 2 z^-2 + 3 z^-3 + 4 z^-4
B(z) = 3 z⁴ + z² + 2 z + 5 + 2 z^-1 + 4 z^-4
C(z) = 3 z⁴ - 3 z³ + 2 z² - 2 z + 1 - z^-1 + z^-4

Dans la pratique, nous trouvons essentiellement des systèmes causaux, c’est-à-dire dont la réponse est consécutive à une sollicitation, donc où les variables complexes z sont toutes à exposants négatifs.

Cependant, dans le cas des filtres récursifs il est fréquent d’exprimer la relation entre l’entrée et la sortie sous la forme d’un quotient à variables z avec des exposants positifs. Une réécriture de la formule montre cependant que seuls les échantillons antérieurs entrent en compte dans le calcul, comme dans l’exemple qui suit.

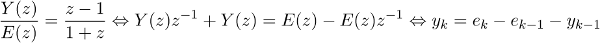
${Y(z) \over{E(z)}}={{z-1}\over{1+z}} \Leftrightarrow Y(z) z^{-1} + Y(z) = E(z) - E(z) z^{-1} \Leftrightarrow y_k = e_k - e_{k-1}- y_{k-1}$

Exemple de quotient en z et sa formule récursive

Maintenant que nous avons l’outil, nous pouvons envisager de transposer le filtre PID dans le domaine numérique.

Intégrale et dérivée

Il y a de très nombreuses manières de calculer une intégrale numériquement. Une large part d’entre elles nécessitent la connaissance de la formule mathématique de la courbe et parfois la connaissance des échantillons postérieurs au point de calcul. Ces méthodes sont utilisées dans les simulations numériques, ou pour calculer des intégrales précisément lorsque la primitive n’est pas déterminable. Elles donnent d’excellents résultats, mais ne peuvent pas être utilisées dans notre contexte.

Il nous faut une approximation de l’intégrale qui puisse être construite à mesure que les échantillons sont prélevés. Pour cela, trois méthodes simples sont généralement envisagées.

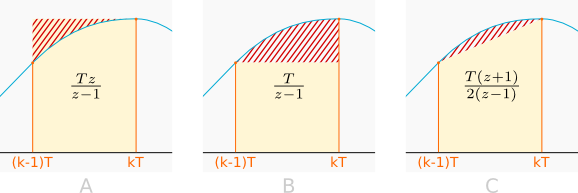
A: Approximation rectangulaire devancée
B: Approximation rectangulaire
C: Approximation trapézoïdale

Dans les diagrammes ci-dessus, nous avons une courbe continue dont nous prélevons des échantillons. Nous voulons en calculer l’intégrale qui est géométriquement l’aire sous la courbe. Nous nous intéressons à une portion d’intégrale entre les échantillons k-1 et k.

L’intégrale calculée par la méthode est représentée en jaune clair. Son erreur est représentée par des hachures rouges. Nous voyons que l’approximation trapézoïdale est généralement meilleure que les deux autres au prix d’un calcul légèrement plus complexe.

Dans notre application, cette complexité impactera les calculs d’initialisation seulement. Nous choisissons donc cette méthode d’estimation de l’intégrale.

En ce qui concerne la dérivée, il n’y a pas d’ambiguïté. En partant de la définition, nous avons une estimée immédiate.

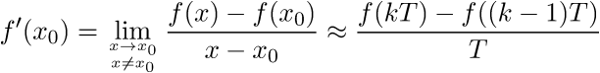
$f'(x_0) = \lim_{x \to x_0\atop x\ne x_0}{f(x)-f(x_0) \over x-x_0} \approx {{f(kT) - f((k-1)T)}\over{T}}$

Définition et approximation de la dérivée

Dans le domaine Z, cela donne simplement 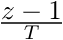(z-1)/T .

Il reste maintenant à combiner ces informations pour obtenir notre filtre PID discret.

PID dans le domaine Z

Commençons par définir le PID dans le domaine continu. Il faut noter que cette définition n’est pas celle que l’on retrouve le plus souvent. Elle est toutefois intéressante, car le terme Kp agit sur l’ensemble de la réponse, ce qui permet d’avoir une réaction à la variation du gain plus intuitive lors des réglages.

$K_P \left[ e(t) + K_I \int_t e(t) + K_D {\mathrm{d} e(t) \over \mathrm{d}t} \right]$

Formule du PID (en temps continu)

Remplaçons l’intégrale et la dérivée par les formules dans le domaine Z précédemment trouvées.

$Y(z) = K_P \left[ E(z) + K_I {{{T \over 2} {{z+1} \over {z-1}}}} E(z) + K_D E(z) {{z - 1} \over T} \right]$

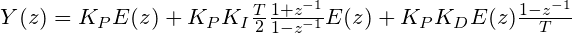
$Y(z) = K_P E(z) + K_P K_I {{{T \over 2} {{1+z^{-1}} \over {1-z^{-1}}}}} E(z) + K_P K_D E(z) {{1-z^{-1}} \over T}$

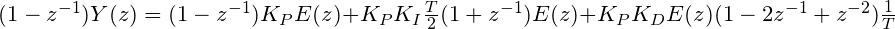
$({1-z^{-1}}) Y(z) = ({1-z^{-1}}) K_P E(z) + K_P K_I {T \over 2} ({1+z^{-1}}) E(z) + K_P K_D E(z) ({1-2 z^{-1}+z^{-2}}) {1 \over T}$

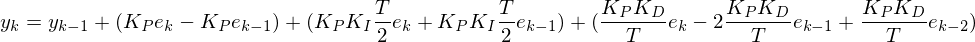
$y_k = y_{k-1} + (K_P e_k - K_P e_{k-1}) + (K_P K_I {T \over 2} e_k + K_P K_I {T \over 2} e_{k-1}) + ({{K_P K_D} \over T} e_k - 2 {{K_P K_D} \over T} e_{k-1} + {{K_P K_D} \over T} e_{k-2})$

Développement du calcul

D’où, par regroupement des termes, la formule récursive :

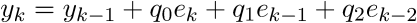
$y_k = y_{k-1} + q_0 e_k + q_1 e_{k-1} + q_2 e_{k-2}$

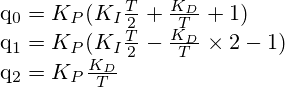
$q_0 = K_P (K_I {T \over 2} + {K_D \over T} + 1) \\ q_1 = K_P (K_I {T \over 2} - {K_D \over T} \times 2 - 1) \\ q_2 = K_P {K_D \over T}$

Formule du PID (en temps discret)

Les coefficients q0, q1, q2 sont des constantes dont la valeur peut être précalculée. Cette formule est alors simple à exécuter. Si le processeur utilise une FPU, il n’aura que trois additions et trois multiplications à faire. S’il dispose en plus des opérations multiplication-accumulation sur flottants, le calcul s’effectue en trois FMAC seulement.

Classe DiscretePID

Pour implémenter cette formule, il faut garder en mémoire les coefficients q0, q1 et q2 ; les valeurs de l’erreur aux temps précédents em1 et em2 ; la valeur de la sortie y. Ces données seront les membres privés de la classe.

Côté membres publics, nous aurons besoin d’un constructeur qui initialisera les coefficients à partir des coefficients exprimés sous la forme classique Kp, Ki, Kd et les autres variables privées à 0. Nous utiliserons aussi une fonction process appelée à chaque échantillon qui prendra en entrée l’erreur et retournera la sortie du filtre.

Ce qui nous donne le prototype de classe suivant.

/** Class to compute PID control filter in discrete form **/
class DiscretePID { 
	private: 
		float q0,  ///< Q0 coefficient
		      q1,  ///< Q1 coefficient
		      q2,  ///< Q2 coefficient
		      em1, ///< Error at previous sample
		      em2, ///< Error two samples ago
		      y;   ///< Filter's output
	public:
		/** Initialize PID filter
		  * @param [in] dt Sampling period in seconds
		  * @param [in] Kp Proportionnal coefficient
		  * @param [in] Ki Integral coefficient
		  * @param [in] Kd Derivative coefficient
		  */
		DiscretePID(float dt, float Kp, float Ki, float Kd); 

		/** Process sampled value
		  * @note Should be called only once per sample
		  * @param [in] error Sampled error
		  * @return Filters's output
		  */
		float process(float error); 
};

En ce qui concerne l’implémentation, le code est trivial.

DiscretePID::DiscretePID(float dt, float Kp, float Ki, float Kd) : 
	q0(Kp*(Ki*dt/2+Kd/dt+1)), 
	q1(Kp*(Ki*dt/2-Kd/dt*2-1)), 
	q2(Kp*Kd/dt), 
	em1(0), 
	em2(0), 
	y(0) { 
} 

float DiscretePID::process(float e) { 
	y += q0 * e + q1 * em1 + q2 * em2; 
	em2 = em1; 
	em1 = e; 
	return y; 
}

Un petit test

Pour illustrer l’utilisation de la classe, et pour observer son comportement, nous allons coder une rudimentaire simulation d’un premier ordre de gain statique 1 et de constante de temps 1s. Même si le code cette simulation tient en une ligne, nous n’allons pas expliquer son fonctionnement ici (voir l’article dédié).

Imposons deux sollicitations sur deux systèmes identiques. La première sera un simple échelon de valeur 1, la seconde sera la sortie du PID dont la consigne est 1. Le calcul des valeurs se fera toutes les 10ms dans une boucle de 5 secondes. Cela mène au code C++ suivant :

float dt = 10e-3; // 10ms
float cmd;
float process1_y = 0;
float process2_y = 0;
DiscretePID pid(dt, 2, 10, 0);

for (float t = 0; t < 5; t += dt) {
	cmd = 1;
	process1_y = cmd + (process1_y - cmd) * 0.99004983; // 1st order discrete equation, K=1, tau=1s @ 10ms

	cmd = pid.process(1 - process2_y);
	process2_y = cmd + (process2_y - cmd) * 0.99004983; // 1st order discrete equation, K=1, tau=1s @ 10ms

	cout << t << ' ' << process1_y  << ' ' << process2_y << endl;
}

Sur ce système du premier ordre, le PID est volontairement (très) mal réglé de sorte à créer des oscillations. Les courbes obtenues montrent bien l’action du correcteur PID qui dans ce cas converge en oscillant.

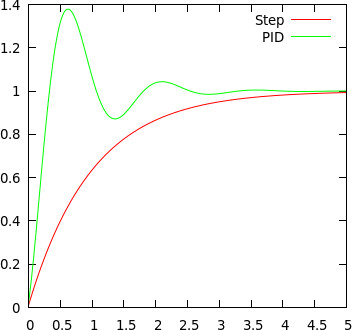
Courbes simulées

Simulation du système avec un échelon et un PID mal réglé

Pour aller plus loin…

Une grande partie des microcontrôleurs ne disposent pas de FPU. Sur ces machines, le calcul flottant est émulé, ce qui se traduit par de nombreux cycles d’horloge consommés. La plupart du temps, ces cycles supplémentaires ne sont pas une réelle gêne. Toutefois dans certains cas, cela peut poser des problèmes de performances.

Dans de tels cas, la classe peut facilement être adaptée pour utiliser des nombres fractionnels simples, ou nombre fractionnels avec décalage d’échelle. Ce cas ne sera pas traité dans cet article, mais la modification reste relativement simple.

Šikula Robotik – Les Eaux – 45 rue de la Bergerie – 85440 TALMONT ST HILAIRE – sikula.robotik@gmail.com – http://sikula-robotik.desbwa.org/

Évènements…

Projets