Base de connaissances Šikula Robotik

Simulation numérique en temps réel

par Florent, mai 2015

Cet article présente les bases d’une simulation dynamique des déplacements du robot en temps réel*. C’est en raffinant les principes exposés ici que nous avons réalisé notre simulateur sur lequel l’asservissement du robot tourne (et anecdotiquement sur lequel nous avons réglé les paramètres d’asservissement du robot 2015 qui ont fonctionné sans modification sur le vrai robot).

Nous verrons d’abord comment simuler grossièrement un moteur à l’aide d’équations du premier ordre et donner à cette simulation les caractéristiques physiques du robot. Nous parlerons aussi des non linéarités majeures qui altèrent la réponse du modèle linéaire mathématique et de quelques éléments de cinématique pour décrire le mouvement global du robot sur la table de jeu.

Avertissement: L’utilisation d’un simulateur dynamique ne convient pas à tous. Il s’agit d’un surplus de temps de travail qui n’est pas utilisé pour le vrai robot. L’avantage principal de ce type de simulation est de pouvoir exécuter la boucle d’asservissement sur le PC. Cela signifie aussi qu’il faut garder le simulateur à jour si une modification est faite sur le robot, que l’asservissement doit savoir gérer les deux plateformes sans quoi il n’y a plus de simulation utilisable (ou de robot). Cela ne dispense pas des tests sur la vraie machine.

* L’expression "temps réel" est utilisée ici dans le sens où les réactions des moteurs sont calculées à mesure que les échantillons de commande arrivent.

La transformée en Z pour les systèmes en temps discret

Nous allons simuler des équations différentielles continues dans un système à temps discret, c’est-à-dire qui découpe le temps en intervalles pendant lesquels il n’a qu’une seule mesure du système supervisé. Le signal est échantillonné et le comportement entre deux échantillons est inaccessible. Toutefois, si la période est suffisamment faible au regard de la dynamique du signal observé, le comportement hors échantillons peut souvent être négligé.

Pour traduire l’évolution temporelle des systèmes échantillonnés, la transformée en Z est un outil mathématique commode. Elle repose sur une fréquence d’échantillonnage fixe caractérisée par une période T. Mathématiquement F(z), transformée en Z de f, peut être définie à partir de la transformée de Laplace de variable s :

F(z) = {{\mathcal{L}[f(t)]}_{ s={{ln z}\over{T}}}} = \sum\limits_{k \in \mathbb{Z}} f(kT) z^{-k}

Transformée en Z de f

La seconde notation sous la forme d’une somme est cependant plus simple à comprendre : le signal est constitué d’un ensemble d’échantillons pris au temps k×T, la variable z servant à indiquer le décalage temporel (retard) dans le signal. Les exemples simples qui suivent permettent de représenter graphiquement le concept.

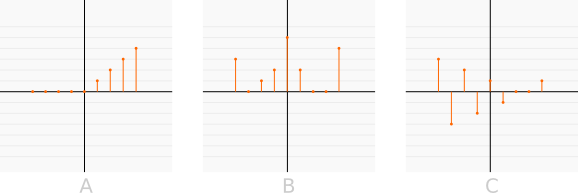
Exemples de signaux.
A(z) = z-1 + 2 z-2 + 3 z-3 + 4 z-4
B(z) = 3 z4 + z2 + 2 z + 5 + 2 z-1 + 4 z-4
C(z) = 3 z4 - 3 z3 + 2 z2 - 2 z + 1 - z-1 + z-4

Dans la pratique, nous trouvons essentiellement des systèmes causaux, c’est-à-dire dont la réponse est consécutive à une sollicitation, donc où les variables complexes z sont toutes à exposants négatifs.

Cependant, dans le cas des filtres récursifs il est fréquent d’exprimer la relation entre l’entrée et la sortie sous la forme d’un quotient à variables z avec des exposants positifs. Une réécriture de la formule montre cependant que seuls les échantillons antérieurs entrent en compte dans le calcul, comme dans l’exemple qui suit.

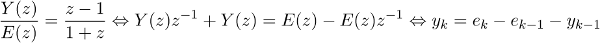
{Y(z) \over{E(z)}}={{z-1}\over{1+z}} \Leftrightarrow Y(z) z^{-1} + Y(z) = E(z) - E(z) z^{-1} \Leftrightarrow y_k = e_k - e_{k-1}- y_{k-1}

Exemple de quotient en z et sa formule récursive

Maintenant que nous avons l’outil, nous pouvons envisager de simuler une équation du premier ordre dans le domaine numérique.

Simulation d’un premier ordre

L’idée est de simuler la vitesse du moteur (rad/s, tics/s, tics/intervalle…) en réponse à la sollicitation (tension, pourcentage de PWM, valeur d’un registre de PWM…). Les unités que vous choisissez doivent être cohérentes mais n’ont pas d’importance capitale dans les discussions qui vont suivre. Cela changera seulement la valeur (et l’unité) de la constante K.

Mais voilà, combinez les équations différentielles électriques et mécaniques du moteur, jouez un peu avec, et vous prouverez sans grand problème que la dynamique de celui-ci n’est absolument pas du premier ordre. Alors pourquoi tout de même simuler une telle équation différentielle ?

Nous pourrions dire que parmi les pôles de l’équation complète, un seul pôle est dominant. Nous pourrions dire que l’inertie de la partie mécanique est très grande devant l’inertie électrique. Nous pourrions dire que dans la dynamique de commande que nous utilisons, certains modes ne sont pas excités. Nous pourrions dire que l’effet des paramètres d’ordre supérieur à 1 est négligeable… Toutes ces raisons sont probablement justes, mais c’est une considération bien plus terre-à-terre qui motive ce choix : donnez un échelon au moteur et il se comporte grossièrement comme un système de premier ordre.

La superbe équation différentielle qui décrit un tel système de premier ordre, avec u(t) l’entrée et y(t) la sortie, va comme suit:

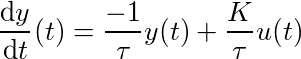
{{\mathrm{d} y \over \mathrm{d} t} (t)} = {-1 \over \tau} y(t) + {K \over \tau} u(t)

Équation différentielle de premier ordre

L’équation est paramétrée par deux grandeurs : Le gain statique K et la constante de temps τ. Ces deux paramètres sont mis en évidence en imposant un échelon [u(t) = constante]. La constante de temps est liée au temps que met le système à se stabiliser (c’est le dénominateur dans l’exponentielle de la solution de l’équation dans le domaine continu), tandis que le gain statique est le rapport y/u quand le système se stabilise à l’infini. Pour les gens pressés, l’infini commence proche de 5×τ.

Avec la transformée en Z, nous retrouvons l’équivalent dans le domaine discret :

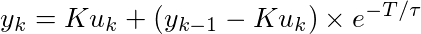
y_k = K u_k + (y_{k-1} - K u_k) \times e^{-T/\tau}

Équation du premier ordre dans le domaine discret

Classe SimFirstOrder

Pour implémenter cette formule, il faut garder en mémoire le gain statique K ; la valeur de l’exponentielle qui est une constante fonction de l’échantillonnage et de la constante de temps du moteur ; la valeur de la sortie y. Ces données seront les membres privés de la classe.

Côté membres publics, nous aurons besoin d’un constructeur qui calculera la valeur de l’exponentielle, stockera la valeur de K, initialisera la sortie à 0. Nous utiliserons aussi une fonction process appelée à chaque échantillon qui prendra en entrée la commande moteur et retournera la sortie en vitesse.

Ce qui nous donne le prototype de classe suivant.

/** Class to simulate first order system **/
class SimFirstOrder { 
	private: 
		float E, ///< Constant, depending on sampling rate and time constant
		      K, ///< Static gain
		      y; ///< Last output
	public:
		/** Initialize first order simulator
		  * @param [in] period Sampling period
		  * @param [in] tau    System time constant
		  * @param [in] k      System static gain
		  */
		SimFirstOrder(float period, float tau, float k = 1);

		/** Compute the system response
		 * @param [in] c Command to apply
		 * @return New value
		 */
		float process(float c);
};

En ce qui concerne l’implémentation, le code est trivial.

SimFirstOrder::SimFirstOrder(float period, float tau, float k) : 
	E(exp(-period / tau)), 
	K(k), 
	y(0) { 
} 

float SimFirstOrder::process(float c) {
	y = K * c + (y - K * c) * E;
	return y;
}

Un petit test

Pour illustrer l’utilisation de la classe, et pour observer son comportement, nous allons vérifier la réaction du simili-moteur à un échelon de valeur 5. Le calcul des valeurs se fera toutes les 10ms dans une boucle de 5 secondes. Cela mène au code C++ suivant :

float dt = 10e-3; // 10ms
SimFirstOrder sim(dt, 0.5, 1);

for (float t = 0; t < 5; t += dt) {
	float out = sim.process(5);
	cout << t << ' ' << out << endl;
}

Sur ce système du premier ordre, le gain statique est de 1 et l’échelon de 5 donc le système converge vers la valeur 5, La constante de temps étant de 500ms, le système atteint 99% de la commande au bout de 2.5s.

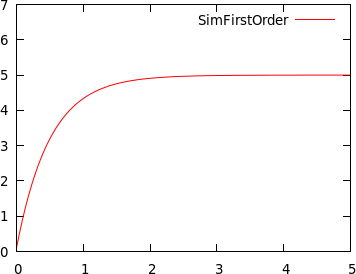
Courbe simulée

Simulation du système avec un échelon de 5

Dans le cas présent, la réponse du moteur est calculé dans le temps de la simulation qui est plus rapide que le temps de la réalité (il faut quelques millisecondes pour calculer et afficher 5s de simulation). Pour obtenir une simulation qui se déroule à la même vitesse que la réalité, il suffit de ralentir la boucle pour qu’elle fasse un tour toutes les 10ms. Sur notre simulateur, nous utilisons la fonction sleep de l’OS. Cette fonction est totalement imprécise, ce qui introduit une petite erreur variable (cela rend la simulation volontairement moins "idéale").

Caractérisation

C’est bien beau tout ça, mais il est où mon robot là-dedans ? Pour que la simulation soit assez fidèle aux déplacements du robot, il faut caractériser ce dernier. Autrement dit, il va falloir trouver le gain statique et la constante de temps liée aux deux moteurs.

Ces valeurs dépendent de beaucoup de paramètres dont voici quelques exemples: résistance des moteurs, système de transmission, répartition des masses dans le robot, ponts en H, codeurs, méthode de calcul de la vitesse… Vu tous les éléments qui entrent en jeu dans la chaîne, mieux vaut faire une mesure approximative que de fumeux calculs. Pour les mêmes raisons, mieux vaut faire la mesure sur le robot complet, et pas seulement sur une base roulante.

Pour déterminer le gain statique de chaque moteur, il suffit d’appliquer un échelon et mesurer la valeur de la vitesse "stabilisée". Le gain est alors le rapport de la vitesse sur la commande. L’unité de ce gain dépend des unités de la commande et de la mesure.

Pour la constante de temps, plusieurs méthodes existent et peuvent être confrontées. La constante de temps correspond à la dérivée à l’origine (au moment de l’échelon) ; au bout de la constante de temps, 63,2% de la sortie est atteinte ; à 3×τ ce pourcentage est de 95,0% ; à 5×τ ce pourcentage est de 99,3%.

Par exemple sur la capture suivante, imaginons que l’échelon était de 20%. Le système se stabilise à 0.1128m/s, soit un gain statique de K=0.1128/0.2=0.564 ; par ailleurs, les 63.2% de la valeur finale sont atteints en τ=125ms. Nous avons les paramètres de simulation du premier moteur, et pouvons appliquer la même méthode pour le second.

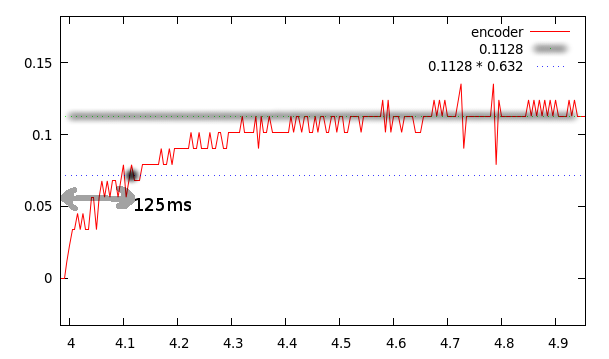
Courbe moteur mesurée

Simulation du système avec un échelon de 5

Notez qu’un bon asservissement est tolérant aux variations du modèle (sur un classique PID, prendre des marges de phase et de gain suffisants). Il n’est donc probablement pas nécessaire d’avoir un modèle de simulation extrêmement précis.

Quelques non linéarités

Réduire un moteur à une équation différentielle linéaire est une modélisation très grossière, mais qui fonctionne étonnamment très bien.

Cependant, un contrôleur pourrait être tenté d’appliquer une commande très élevée qu’il n’est pas possible d’appliquer avec la carte de commande (et c’est probablement mieux ainsi). Pour que le simulateur se comporte comme le robot, il est nécessaire d’insérer une non linéarité en limitant au préalable l’entrée. Dans notre cas, une simple saturation de la commande entre -100% et +100% fonctionne bien.

Nous prenons également en compte une zone morte. Il s’agit d’une plage de valeur de PWM autour de zéro dans laquelle la commande est ramenée à zéro. Elle correspond à la zone où le moteur n’a pas assez de couple pour modifier sa vitesse.

Une réflexion sur la discrétisation (en valeur) des signaux est à avoir également. De notre côté, nous avons fait le choix de maintenir la précision des variables internes à la simulation, et discrétiser les signaux de commande PWM et de retour codeurs afin d’avoir une mesure de simulation proche de la mesure qui aurait été faite réellement.

Cinématique

Maintenant que la vitesse de chaque moteur est simulée, il est possible de les passer dans un modèle cinématique pour déduire la position par exemple. En réalité, faire ce calcul dans la simulation a un intérêt limité puisqu’il est tout à fait envisageable d’utiliser l’odométrie du progamme du robot.

Pour notre part, calculer la position à la fois dans l’odométrie (avec les valeurs discrétisées) et dans le simulateur (avec la précision complète) nous a permis d’ajuster les calculs de l’odométrie pour minimiser l’impact de la discrétisation. Depuis plusieurs années, la position du simulateur n’est plus utilisée du tout.

Les équations cinématiques sont exactement les mêmes que pour l’odométrie. En résumé, la moyenne des vitesses des moteurs (éventuellement à multiplier par une constante) donnent la vitesse moyenne longitudinale du robot. Leur différence (à multiplier par une constante) donne une vitesse angulaire. Les constantes évoquées dans les relations précédentes permettent de faire la conversion dans une unité commode (dans notre cas, m/s et rad/s).

La vitesse angulaire permet de retrouver l’angle par intégration.

La vitesse longitudinale multipliée par le cosinus de l’angle donne la vitesse projetée sur l’axe x ; multipliée par le sinus de l’angle donne la vitesse projetée sur l’axe y. Par intégration, nous retrouvons les positions x et y.

Pour aller plus loin…

Nous vous avons présenté ici les bases du simulateur dynamique. L’implémentation de ces idées, et surtout l’interfaçage de celles-ci avec le code existant, ne sont pas totalement triviaux. Par ailleurs, une fois le mécanisme en place, il faut encore comparer le comportement simulé et le comportement réel et ajouter à la simulation les "imperfections" qui ont un effet important sur le déplacement de votre robot, ainsi que les éventuelles spécificités liées à votre environnement.

Il est bon de rappeler que cet outil est très pratique, mais qu’il ne remplace pas les tests sur le robot. Pour notre part, il a un intérêt pour des expérimentations sur l’asservissement (nous avons souvent "cassé" le robot simulé). Il sert également comme simulateur cinématique classique pour l’intelligence, à la différence près que les profiles de déplacement complexes s’exécutent en des temps proches des temps réels de déplacement du robot. Un inconvénient majeur est que lorsque la machine a peu de ressources disponibles (machine virtuelle chargée par exemple), il arrive que la simulation ne fonctionne plus du tout comme attendu.

Šikula Robotik – Les Eaux – 45 rue de la Bergerie – 85440 TALMONT ST HILAIRE – sikula.robotik@gmail.com – http://sikula-robotik.desbwa.org/