Base de connaissances Šikula Robotik

Odométrie : savoir où le robot se trouve

par Florent, mai 2018

Cet article présente le système d’odométrie que nous utilisons pour connaître la position de notre robot. Si le code en lui-même est en vérité très court, les sujets qu’il soulève sont extrêmement riches si bien que tout ne peut être traité dans un tel article. Néanmoins, outre les présentations générales qui sont de mise, nous avons décidé d’approfondir quelques aspects qui améliorent grandement la précision de l’estimation de position.

Le principe

Imaginez que vous faites 4 pas vers l’azimut 126.87° (valeur choisie pour tomber juste sur le dessin) puis 3 pas sur votre gauche à angle droit. Vous pouvez facilement conclure que vous vous trouvez désormais à 5 pas pile à l’est de votre position initiale. Tout du moins si vous acceptez de penser que vos pas sont suffisamment petits pour négliger la courbure de la Terre, suffisamment grands pour négliger les petites aspérités du terrain, suffisamment réguliers pour l’expérience de pensée, suffisamment… bref.

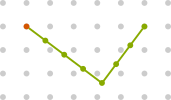
Illustration du chemin parcouru

D’une manière analogue et avec un peu de trigonométrie, le robot va retrouver sa position actuelle à l’aide des déplacements qu’il a faits depuis la dernière position connue. En quelque sorte, il va lui aussi « compter ses pas ».

Pour ce faire, le robot est doté de deux roues qui viennent en supplément des roues de propulsion. Elles sont alignées avec ces dernières et montées sur des capteurs appelés codeurs qui mesurent leur déplacement angulaire. De plus, un système mécanique assure que ces roues touchent en permanence le sol. Ainsi, à chaque mouvement du robot, les deux petites roues libres se mettent à faire tourner les codeurs et le déplacement qu’ils détectent est utilisé pour estimer le mouvement global.

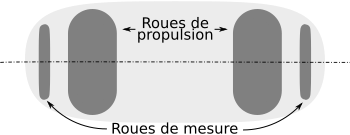
Position des roues, vue de dessus

Dès lors, il faut distinguer la position estimée par le robot de sa position réelle sur le terrain. Le système d’odométrie fonctionnant nécessairement par intégration (on accumule des petits déplacements), ces deux positions peuvent facilement dériver. Malgré ce jeu de mot facile, il s’agit d’un problème sérieux, car le robot peut se retrouver rapidement perdu.

Tout l’enjeu consiste donc à maîtriser les erreurs inhérentes afin de limiter au maximum la divergence vis-à-vis de la position réelle au cours du temps, sans quoi des recalages fréquents sont à prévoir. Dans le contexte de la coupe de France de robotique où le temps de match est limité, il est possible de réduire suffisamment l’écart pour qu’il soit négligeable jusqu’à la fin de la partie ; mais il faut être rigoureux.

Cinématique

Mesure

Nous supposerons ici que le décodage des signaux des codeurs existe par ailleurs et que la valeur de ceux-ci peut être utilisée. Il est critique de faire un relevé à période régulière à faible gigue (tâche de haute priorité ou interruption) pour avoir une mesure fiable dont dépendra le reste des calculs. Une fois la mesure réalisée, les calculs n’ont pas de contrainte de temps particulière si ce n’est que le résultat doit être disponible pour la prochaine itération.

La fréquence d’échantillonnage choisie doit être compatible avec les données traitées. Par exemple, si les codeurs ont beaucoup d’impulsions par tour ou si le robot se déplace rapidement (ou les deux), la fréquence doit être assez élevée pour que le nombre de tics mesuré pendant la période ne soit pas trop grand pour ne pas faire déborder les calculs mais aussi pour que l’approximation ne soit pas trop grossière. A contrario, il ne faut pas une fréquence trop élevée au risque de ne plus avoir assez de donnée par échantillon pour que l’approximation ait un sens.

Pour notre robot, une fréquence de 100Hz ou 200Hz donne de bons résultats. De plus, cela est compatible avec la dynamique de nos moteurs, dans le sens où les variations de vitesse (temps de montée suite à un échelon par exemple) sont bien observables sur la mesure.

Notons par ailleurs que la mesure est réalisée sur des roues séparées de la propulsion alors qu’il serait possible d’utiliser des codeurs directement montés sur les moteurs. En procédant ainsi, nous ne perdons pas la position si les roues patinent, par exemple à cause d’un asservissement un peu trop agressif ou d’un obstacle.

Observation

Commençons par observer ce qu’il se passe lorsque nous bougons le robot manuellement. Lorsque le robot se déplace en ligne droite vers l’avant, les deux codeurs indiquent la même vitesse positive. En arrière, la même vitesse négative. En tournant sur lui-même, les vitesses gauche et droite sont opposées et le signe de leur différence indique le sens (trigonométrique ou horaire). Il est donc tout à fait possible d’utiliser ces mesures pour savoir ce que le robot fait dans ces cas simples.

Exemples de mesure : avance droit, recule droit, tourne sur lui-même sens trigonométrique, tourne sur lui-même sens horaire

Lorsque le mouvement est plus complexe, un arc de cercle par exemple, il ne faut pas longtemps pour s’apercevoir que la mesure faite par les codeurs est une composition des cas simples vus auparavant : le mouvement est décomposable en translation (sur la trajectoire curviligne) et en rotation. Pour cela, il suffit de prendre la moyenne des retours codeurs pour avoir la vitesse curviligne et leur différence pour déduire la vitesse de rotation.

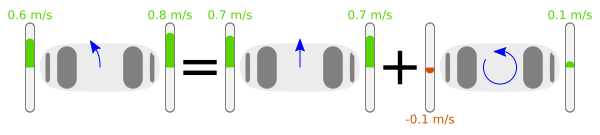
Exemple de décomposition d’une mesure

Unités

Notez que les retours directs des codeurs sont dans une unité propre à ceux-ci (appelons cette unité tics) divisée par le temps de mesure (par exemple 10 millisecondes). Pour simplifier la compréhension nous convertissons rapidement les valeurs mesurées vers le système international d’unités (mètres par seconde et radians par secondes).

De nombreux éléments entrent en jeu pour relier la mesure en tics au système international. Par exemple le diamètre des roues, leur écartement, le nombre de pas des codeurs, la méthode pour compter ces pas, l’éventuel rapport de réduction, etc. jouent un rôle dans la conversion. Cependant, chaque grandeur étant sujette à une mauvaise mesure, et ces erreurs pouvant s’accumuler, nous préférons utiliser deux constantes qui englobent tout cela dans un seul facteur : le nombre de tics par mètre et le nombre de tics « différentiels » par radian. Ces grandeurs ont l’avantage d’être mesurables à l’aide du robot lui-même.

La méthode pour déterminer ces constantes nécessiterait un article complet à elle toute seule. Néanmoins, nous pouvons l’esquisser. Il est important de commencer par l’angle : faire tourner le robot sur lui-même de nombreux tours et trouver le rapport entre ce qui a été mesuré et l’angle réel effectué. Une fois l’angle juste, le plus simple est d’utiliser l’odométrie en faisant parcourir une ligne droite et en utilisant la distance selon l’axe X (ou Y selon votre convention) pour calculer l’autre rapport. Grâce à l’odométrie, les petits virages effectués seront en effet compensés dans cette mesure.

Utiliser ces unités apporte un confort dans de nombreux domaines comme la simplification des équations, une facilité dans la relecture du code, une simplification de l’analyse des données mesurées, etc. Travailler le plus souvent dans le système international d’unités est en général une bonne idée si les contraintes le permettent. Notre processeur disposant d’une unité arithmétique à virgule flottante, le changement d’unité n’affecte pas significativement le temps de calcul.

Intégration

Maintenant que nous avons la vitesse longitudinale et la vitesse angulaire dans les bonnes unités, c’est facile, il suffit d’intégrer.

Dans notre cas, nous utilisons la transformée en Z de l’approximation trapézoïdale de l’intégrale que nous avons déjà présentée dans un autre article. Elle a l’avantage d’être une méthode de calcul rapide, simple à implémenter, qui traite les échantillons à mesure qu’ils arrivent. Par rapport à la méthode d’accumulation classique (ou approximation rectangulaire devancée : y += v × dt), l’erreur est réduite comme illustré sur la figure suivante (l’intégrale calculée par la méthode est représentée en jaune clair, son erreur est représentée par des hachures rouges).

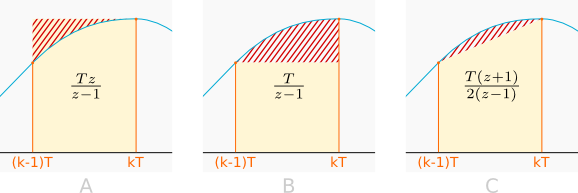
A: Approximation rectangulaire devancée
B: Approximation rectangulaire
C: Approximation trapézoïdale

Ainsi donc, intégrer la vitesse angulaire nous donne l’angle.

À partir de lui, il est facile de projeter la vitesse curviligne. Cette vitesse multipliée par le cosinus de l’angle donne la vitesse projetée sur l’axe x ; multipliée par le sinus de l’angle donne la vitesse projetée sur l’axe y. Par intégration, nous retrouvons les positions x et y.

Le tour est joué.

Ici, il serait d’usage de mettre les formules qui font peur, mais est-ce bien utile après cette explication ?

Améliorer la précision de l’angle

L’angle joue un rôle fondamental dans le calcul de l’odométrie et il nous faut donc le choyer. Pour améliorer la précision globale, nous utilisons plusieurs astuces.

Asymétrie

La première astuce concerne l’asymétrie du diamètre des roues qui est nécessairement présente même avec les procédés mécaniques de précision. Or il se trouve qu’une petite différence de diamètre entre ces roues peut changer perceptiblement la qualité de la mesure. Par exemple, si le robot est guidé en ligne droite, il mesurera malgré tout une trajectoire sur un grand cercle. Ce défaut peut être corrigé logiciellement.

Numériquement, imaginons des roues de respectivement 4.999 et 5.001 centimètres de diamètre écartées de 30 centimètres. Elles mesurent toutes les deux 2 mètres (croyant être à la côte de 5 centimètres) et ont alors parcouru en réalité respectivement 1.9996 et 2.0004 mètres. Cela correspond à un cercle de 750 mètres de rayon parcouru sur un peu plus de 0.15 degrés (qui est aussi l’erreur d’angle), soit une très petite erreur en longitudinal et plus de 2.6 millimètres perpendiculairement à l’axe de déplacement estimé.

L’erreur est assez petite mais va être cumulée (et certainement agrandie) au cours des déplacements suivants.

Pour corriger, nous appliquons un facteur (1+a) et (1-a) aux mesures gauche et droite avant d’effectuer les calculs d’odométrie. La valeur de a est déterminée par mesure sur le robot en effectuant un grand nombre de tours dans les deux sens : si un sens a plus d’erreur que l’autre, il faut corriger. D’ailleurs, la valeur des codeurs révisée par ce facteur est également utilisée dans l’asservissement.

Petites détections

Un choix mécanique aide également pour la précision de l’angle et de l’odométrie en général.

Nous utilisons de petites roues de mesure : plus elles sont petites, plus elles font de tours pour la même distance parcourue. Cela permet d’augmenter sensiblement la résolution (à la fois en distance et en angle). Par ailleurs, nous n’utilisons pas de système de réduction entre la roue et le codeur pour éviter tout jeu.

Pour augmenter la résolution angulaire, il convient d’espacer au maximum les roues de mesure. Cette fois-ci, c’est parce qu’elles parcourent plus de distance (donc plus de tics) pour un même angle effectué.

Dans notre cas, les vibrations produites par un coup de poing sur la table suffisent à faire bouger la mesure. Attention toutefois, plus de résolution signifie de plus grands nombres à traiter. Il faut que le système de mesure et de traitement des données puisse gérer ceux-ci.

À titre d’exemple, il nous est arrivé d’avoir une simulation complètement chaotique à haute vitesse. En fait, nous avions augmenté les performances du robot et tout se passait bien en réel. Mais le simulateur simulait toujours l’ancien système de mesure qui était sur 8 bits, pas assez pour les nouvelles capacités du robot.

Intégration

Avant de passer au pseudo code, il faut noter que nous intégrons la vitesse gauche et droite pour obtenir la distance totale parcourue par chaque roue, et que ces valeurs servent à déduire l’orientation du robot par simple soustraction. En effet, l’angle du robot est totalement indépendant de la trajectoire parcourue.

Il s’agissait originellement d’une astuce dont l’application apportait un gain phénoménal sur l’odométrie. Rétrospectivement, nous supposons que ce gain était dû à une autre erreur dans le code, corrigée depuis, puisque les simulations montrent aujourd’hui qu’il n’y a finalement aucun de gain réel avec cette méthode. Nous gardons néanmoins cette pratique, car le code n’a pas été modifié depuis sa création.

Pseudo code

Pour résumer tout ça, voici un pseudo code.

En entrée, nous avons les mesures des codeurs corrigés de leur asymétrie (meas_left_corrected et meas_right_corrected). En sortie, nous avons x et y qui sont de type Integral exprimés en mètres ainsi que theta l’angle de robot en radians. Il y a aussi des intégrales auxiliaires il et ir, respectivement pour les intégrales de roue gauche et droite, ainsi que les constantes de géométrie tics_per_m et difftics_per_rad et le pas de calcul dt.

Il est supposé que le type Integral prend le pas de calcul en constructeur, dispose d’une méthode process qui réalise le calcul d’intégration avec la nouvelle valeur passée en paramètre et d’une fonction value qui retourne la valeur intégrée courante.

const double dt = 0.010;
const double tics_per_m = 25150.42;
const double difftics_per_rad = 5185.86;

Integral il(dt), ir(dt), x(dt), y(dt);
double theta = 0;
bool run = true;

while (run) {
	// Wait next compute step (this is not a sleep or equivalent : it is a fixed period wakeup)
	wait_next_step_with_precision();

	// Measure
	double meas_left_corrected = get_meas_left_corrected();
	double meas_right_corrected = get_meas_right_corrected();

	// Compute velocities
	double dL = meas_left_corrected / dt;  // Left speed (in tics/s)
	double dR = meas_right_corrected / dt; // Right speed (in tics/s)
	double v = (dR + dL) / 2 / tics_per_m; // Mean speed (in m/s)

	// Compute angle
	il.process(dL);
	ir.process(dR);
	theta = (ir.value() - il.value()) / difftics_per_rad;

	// Update X & Y
	x.process(v * cos(theta));
	y.process(v * sin(theta));
}

Un système autonome

Enfin, il faut noter que sur notre robot l’estimation de position est un système complètement autonome.

Le système d’odométrie fonctionne en permanence dès que le robot est allumé. Il démarre à la position nulle et commence à modifier son estimation au moindre mouvement mesuré. Bien sûr, nous avons la possibilité de replacer son origine manuellement et le programme d’intelligence ne manque pas d’utiliser cette fonction pendant la phase de préparation des matchs de coupe de France de robotique.

En fait, l’odométrie ne se préoccupe pas de ce que fait ou prévoit le reste du robot. En particulier, elle est indépendante du module d’asservissement qui, de son côté, effectue des calculs séparés (avec les mêmes données d’entrée) pour ses propres besoins. Ainsi, le robot est capable d’estimer sa position à tout moment : même si l’asservissement se met à faire des folies, même si nous poussons le robot à la main, même s’il se fait tamponner, même si l’arrêt d’urgence est enclenché. Tout cela à condition que les roues d’odométrie ne glissent pas, évidemment.

L’autonomie de ce système est particulièrement pratique lorsque le robot s’arrête à cause d’un adversaire ou à cause d’une détection de défaut de déplacement. Puisque la position calculée est toujours valide, le programme d’intelligence peut choisir ce qu’il va faire en fonction de la position effective après freinage d’urgence. Nous utilisons aussi cela pour le calage initial contre la bordure (fait à la main) : une fois calé, nous pouvons placer le robot comme bon nous semble dans la zone de départ, et même lui demander de se placer tout seul à sa position de départ optimale avant le match.

Pour aller plus loin…

Disposer en permanence d’une estimation de position valide offre de nombreux avantages et ouvre les possibilités.

Par exemple dans notre cas, la position est en permanence disponible pour l’interface graphique. Ainsi, nous savons visuellement où le robot pense être et pouvons projeter sur une carte les détections des sonars pour vérifier ce qu’il voit. Cela s’avère très utile aussi en simulation où c’est le seul moyen de savoir où il est.

De manière plus utile en match, notre programme d’intelligence s’appuie sur cette position pour effectuer les mouvements : l’asservissement ne connaît que les déplacements relatifs, mais l’intelligence fait la traduction et le cas échéant la décomposition en mouvements élémentaires. Ainsi, du point de vue de la stratégie, des commandes telles que « Va en X,Y », « Aligne-toi à tel azimut » ou même « Va en tel X en gardant le même Y » offrent un confort de programmation indéniable.

À la date où l’article est écrit, nous avons commencé une recherche de chemin automatique qui agrémentera cette panoplie d’outils haut-niveau. Celle-ci s’appuie nécessairement sur la disponibilité de l’information de position courante. La connaissance de sa position peut également servir à changer de choix stratégique si une action est entravée.

Il est à noter que l’odométrie présentée n’effectue pas de modulo sur l’angle. Nous avons choisi de laisser l’information du nombre de tours dans la valeur et de l’ignorer par un modulo dans les couches supérieures si besoin. Par exemple, pour prendre le cap 0, il ne faut pas demander un déplacement relatif de -angle, car le robot pourrait faire plusieurs tours inutiles.

Il est certain que vous aurez beaucoup d’idées une fois ce genre de mécanisme fonctionnel dans votre robot. Mais attention, il ne faut pas négliger le temps de réglage si vous voulez pouvoir vous y fier suffisamment.